
My research interests are generally in uncertainty quantification, at the interface of numerical analysis, approximation theory and statistics. I have worked on the following topics:

Mathematical modelling and simulation are frequently used to inform decisions and assess risk. However, the parameters in mathematical models for physical processes often impossible to determine fully or accurately, and are hence subject to uncertainty. In practice, it is crucial to study the influence of this uncertainty on the outcome of the simulations, in order to correctly quantify risk and make decisions. By assigning a probability distribution to the parameters, which is consistent with expert knowledge and observed measurements if they are available, it is then possible to propagate the uncertainty through the model and quantify the induced uncertainty in the model outputs.
A standard computational method to propagate the uncertainties through the model is to use Monte Carlo sampling (also known as ensemble methods): we pick different realisations of our uncertain parameters, simulate the model for the different scenarios, and make inference on output quantities of interest from the ensemble of simulations. This process can be notoriously time consuming, especially when applied to complex models which result in expensive simulations.
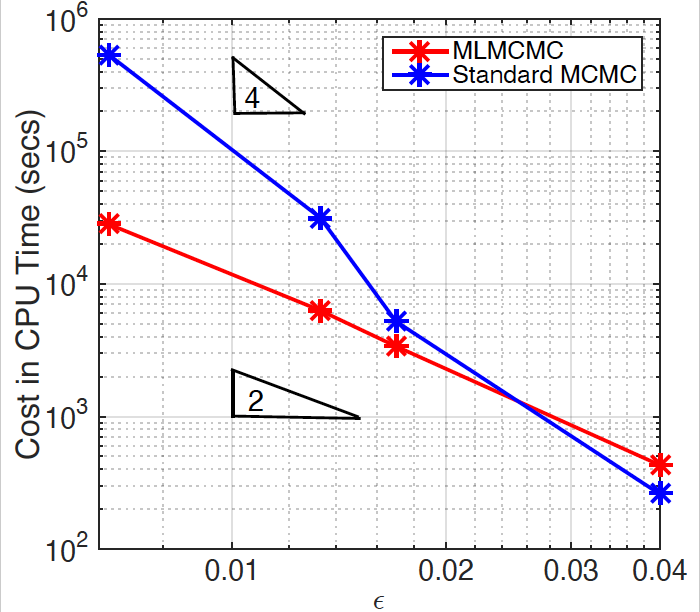
Multilevel Monte Carlo (MLMC) methods alleviate the simulation cost by utilising different discretisations (or approximations) of the underlying models. Most simulations are done with a low cost/low accuracy discretisation to capture the bulk behaviour, while a few high cost/high accuracy simulations are added to increase the overall accuracy.
An example problem is groundwater flow modelling, with potential applications in carbon capture and storage underground. In this setting, the precise make-up of the environment, such as the location and conductive properties of different layers of soil, is not fully known. Darcy’s law for a steady state flow in a porous medium, coupled with incompressibility conditions, results in a diffusion PDE for the flow of water underground. The end goal is to quantify the risk of leaked particles from a repository re-entering the human environment, which requires estimating the unknown hydraulic conductivity, which appears as the diffusion coefficient in the PDE, and subsequently simulating particle flow in the resulting velocity field.
Multilevel methods are extremely powerful, often leading to orders of magnitude savings in computational cost to obtain a given accuracy, and so this is a very active area of research. For an overview of research on multilevel methods, see for example this community webpage. I'm currently interested in developing multilevel methods for Bayesian inference, for multi-scale problems and for chaotic systems.
Sample publications in this area:
-T.J. Dodwell, C. Ketelsen, R. Scheichl, A.L. Teckentrup. Multilevel Markov Chain Monte Carlo. SIAM Review, 61(3), 509-545, 2019.
- R. Scheichl, A.M. Stuart, A.L. Teckentrup. Quasi-Monte Carlo and Multilevel Monte Carlo Methods for Computing Posterior Expectations in Elliptic Inverse Problems. SIAM/ASA Journal on Uncertainty Quantification, 5(1), 493–518, 2017. Available as arXiv preprint arXiv:1602.04704.
- A.L. Teckentrup, P. Jantsch, C.G. Webster, M. Gunzburger. A Multilevel Stochastic Collocation Method for Partial Differential Equations with Random Input Data. SIAM/ASA Journal on Uncertainty Quantification, 3(1), 1046–1074, 2015. Available as arXiv preprint arXiv:1404.2647.
- K.A. Cliffe, M.B. Giles, R. Scheichl, A.L. Teckentrup. Multilevel Monte Carlo Methods and Applications to Elliptic PDEs with Random Coefficients. Computing and Visualization in Science, 14(1), 3-15, 2011.
The parameters in mathematical models for real-world processes are often impossible to measure fully and accurately, due to limitations in for example sensor technology, time or budget. The limited measurements that are available can be combined with expert prior knowledge in a Bayesian statistical framework, resulting in the probability distribution of the unknown parameters conditioned on the measurements, the so-called posterior distribution. In practical applications, the goal is often to compute the expected value of a quantity of interest under the posterior distribution.
Markov chain Monte Carlo (MCMC) methods are the gold standard for sampling from the posterior distribution. However, for complex mathematical models such as those based on PDEs, these methods become prohibitively expensive, since the generation of each sample requires the evaluation of the model and typically many such samples are required. Therefore, there is a pressing need to make the methodology more efficient.
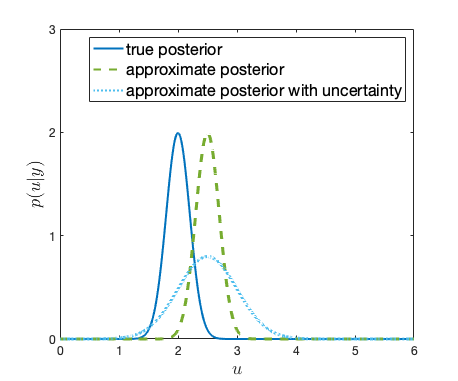
One way to drastically reduce the computational cost of MCMC methods is to develop a multilevel version. For more details, see the topic above. An alternative approach is to use a surrogate model (a.k.a. reduced order model or emulator), replacing the original mathematical model by a simpler, less expensive model, and thus obtaining an approximate posterior distribution that is feasible to sample from in practice.
I'm currently particularly interested in the use of random surrogate models, including those stemming from probabilistic numerical methods, randomised projection methods and Gaussian process regression. These randomised methods allow us to include the error (or uncertainty) between the true and surrogate model in the posterior distribution, and thus avoid over-confident inferences. My work aims to justify the use of random surrogate models from a theoretical point of view, studying well-posedness and stability properties of the posterior distribution, but also addresses the development of efficient algorithms for sampling from the approximate posterior distribution.
I'm also interested in Bayesian inference in complex models in general, and I have for example done some recent work in Bayesian model comparison, where the unknown to be inferred is the model itself rather than a parameter in a given model, with applications in fluid dynamics.
Sample publications in this area:
- M. Brolly, J.R. Maddison, J. Vanneste, A.L. Teckentrup. Bayesian comparison of stochastic models of dispersion Available as arXiv preprint arXiv:2201.01581.
-T.J. Dodwell, C. Ketelsen, R. Scheichl, A.L. Teckentrup. Multilevel Markov Chain Monte Carlo. SIAM Review, 61(3), 509-545, 2019.
- H.C. Lie, T.J. Sullivan, A.L. Teckentrup. Random forward models and log-likelihoods in Bayesian inverse problems. SIAM/ASA Journal on Uncertainty Quantification, 6(4), 1600-1629, 2018. Available as arXiv preprint arXiv:1712.05717.
- A.M. Stuart, A.L. Teckentrup. Posterior Consistency for Gaussian Process Approximations of Bayesian Posterior Distributions. Mathematics of Computation, (87), 721-753, 2018. Available as arXiv preprint arXiv:1603.02004.
Many problems in science and engineering require the reconstruction of an unknown function from a finite amount of training data, often given in terms of a set of input-output pairs. This includes many problems in machine learning, such as the prediction of the output at a new test input, as well as the construction of surrogate models (a.k.a. reduced order models or emulators) to approximate a complicated mathematical model by a simpler model with much lower computational cost.
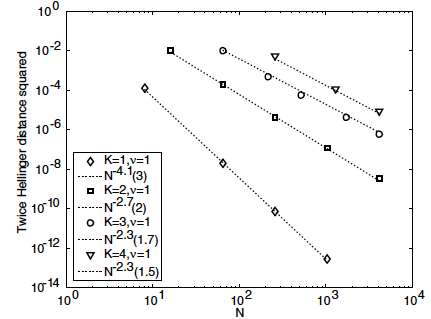
Gaussian process regression is a Bayesian approach to solving this problem. It involves placing a Gaussian process prior distribution on the unknown function, which is then conditioned on the observed training data to obtain the posterior distribution. In my research, I'm interested in the behaviour of the posterior distribution as the amount of training data goes to infinity. Ideally, we want the posterior distribution to concentrate on the "true" underlying function that generated the training data, a concept known as posterior consistency. Under what conditions can this be guaranteed?
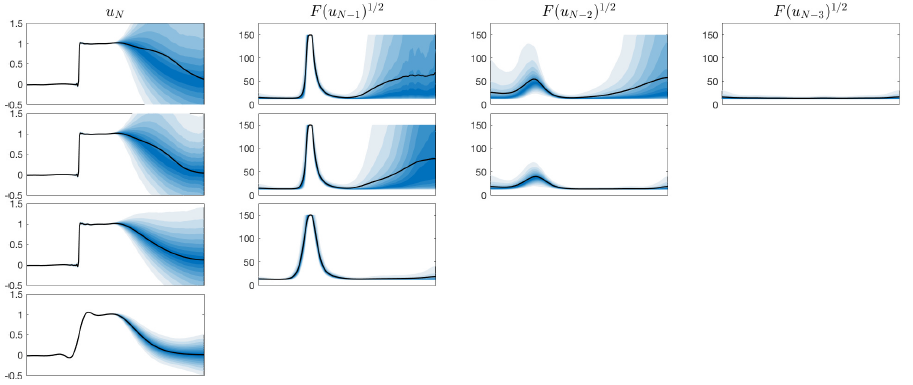
I'm also interested in developing Gaussian process regression for Bayesian inverse problems, where the goal is to use Gaussian process regression to construct a surrogate model to use in a Bayesian posterior distribution. (For more details, see the topic above.)
For optimal performance, the choice of the Gaussian process prior distribution and training data need to adapted to this specific goal. The prior distribution needs to be designed carefully to be able to tackle the high dimensions typically present in inverse problems, and should be constrained to obey physical constraints posed by the underlying model. How can we incorporate this? The training data should be chosen to provide as much information as possible about the posterior distribution. How can we do this efficiently?
Sample publications in this area:
- A.L. Teckentrup. Convergence of Gaussian process regression with estimated hyper-parameters and applications in Bayesian inverse problems. SIAM/ASA Journal on Uncertainty Quantification, 8(4), p. 1310-1337, 2020.
- A.M. Stuart, A.L. Teckentrup. Posterior Consistency for Gaussian Process Approximations of Bayesian Posterior Distributions. Mathematics of Computation, (87), 721-753, 2018. Available as arXiv preprint arXiv:1603.02004.
Hierarchical and deep Gaussian processes are powerful tools to model non-stationary behaviour. These models are based on a sequence of Gaussian processes, often referred to as layers, which are linked through operations such as composition to obtain more sophisticated random processes.
Deep Gaussian processes can be used as prior distributions in Bayesian approaches to regression, allowing the effective recovery of functions with steep gradients and multiple length scales. Similar ideas can be applied to Bayesian quadrature.
In my research, I'm interested in mathematical properties of deep Gaussian processes, including convergence properties as the number of layers or the amount of training data used in regression goes to infinity, as well as algorithmic aspects such as efficient methods for sampling and ways to incorporate anisotropy.
Sample publications in this area:
- M.A. Fisher, C.J. Oates, C.E. Powell and A.L. Teckentrup. A locally adaptive Bayesian cubature method. In International Conference on Artificial Intelligence and Statistics (AISTATS), Proceedings of Machine Learning Research, p. 1265-1275, 2020.
- M.M. Dunlop, M. Girolami, A.M. Stuart, A.L. Teckentrup. How deep are deep Gaussian processes? Journal of Machine Learning Research, 19, 1-46, 2018. Available as arXiv preprint arXiv:1711.11280.