(For a full list see below or go to Google Scholar).

We consider a system in which an ouzo-like liquid coexists with its vapour. Our model allowed the identification of complex bulk phase behaviour. We also determined some interesting features of ternary phase diagrams for systems of this type.
D. N. Sibley, B. D. Goddard, F. F. Ouali, D. J. Fairhurst, and A. J. Archer

We consider a numerical framework tailored to identifying optimal parameters in the context of modelling disease propagation. We derived first order optimality conditions and developed a novel numerical scheme, which we compared to existing approaches.
A. Miniguano-Trujillo, J. W. Pearson, and B. D. Goddard
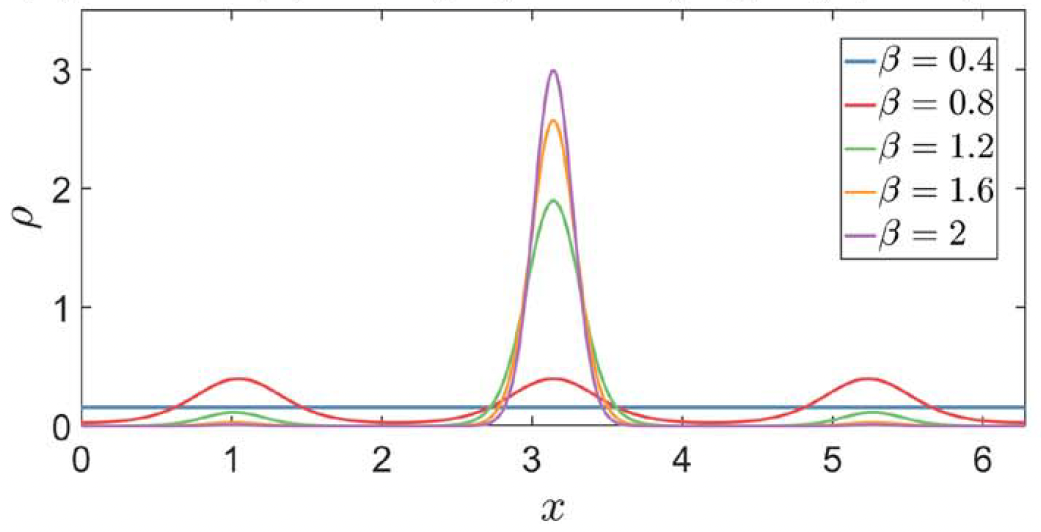
We considered weakly acting diffusions on the torus for multichromatic interaction potentials, determining that the dynamics can exhibit multipeak stationary states, related to the number of nonzero Fourier modes of the interaction. This involved a careful mix of analysis, perturbation theory, and numerics.
B. Bertoli, B. D. Goddard, and G. A. Pavliotis
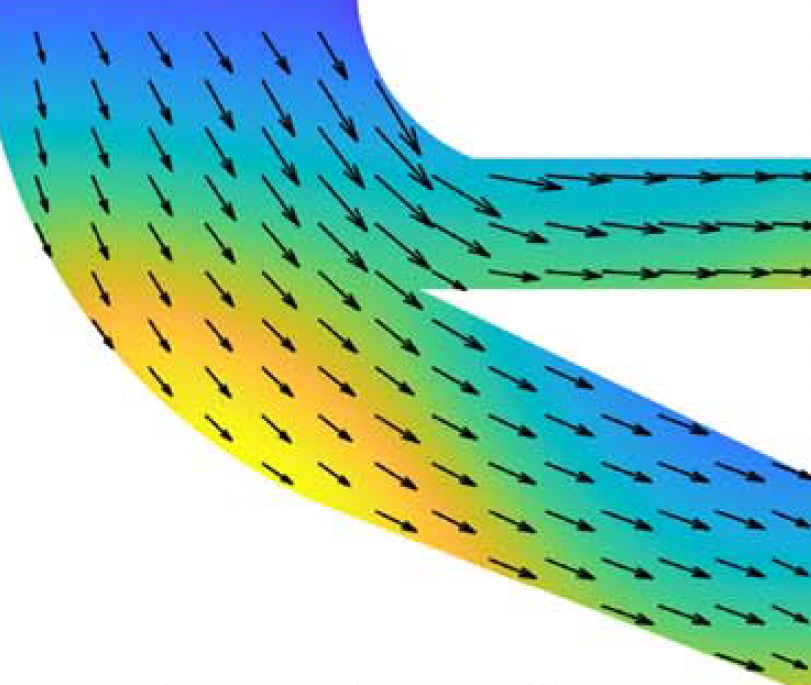
We developed a numerical framework to solve general nonlinear and nonlocal PDEs on complicated two-dimensional fomains. This included an open-source MATLAB implementation. We provided applications in dynamic density functional theory and PDE-constrained optimization.
J. C. Roden, R. D. Mills-Williams, J. W. Pearson, and B. D. Goddard
Efficient nonlocal linear image denoising with NFFT and preconditioning
A. Miniguano-Trijllo, J. W. Pearson, and B. D. Goddard
Changing the flow profile and resulting drying pattern of dispersion droplets via contact angle modification
C. Morcillo Perez, M. Rey, B. D. Goddard, and J. H. J. Thijssen
arxiv
Poisson Equations with locally-Lipschitz coefficients and Uniform in Time Averaging for Stochastic Differential Equations via Strong Exponential Stability
D. Crisan, P. Dobson, B. D. Goddard, M. Ottobre, and I. Souttar
arxiv
[44] Analysing Opinion Dynamics via a Cognitive Model of Structured Beliefs
E. Michaelidou, E. Ioannou, K. Tapper, B. D. Goddard, and G. Romero Moreno
In: Carletti, T., Njougouo, TS., Tuci, E. (eds). Artificial Life and Evolutionary Computation. WIVACE 2024. Communications in Computer and Information Science, vol 2532. Springer, Cham., 2025
[43] On opportunities to study historical linguistics in schools in the United Kingdom
B. D. Goddard, F. Iezzi, P. Iosad, W. Reynolds, and G. Trousdale
Ped. Ling., 6(2) 134-154, 2025
[42] Coexisting multiphase and interfacial behavior of ouzo
D. N. Sibley, B. D. Goddard, F. F. Ouali, D. J. Fairhurst, and A. J. Archer
Phys. Fluids, 37, 042118, 2025
[41] A constrained optimisation framework for parameter identification of the SIRD model
A. Miniguano-Trujillo, J. W. Pearson, and B. D. Goddard
Math. Biosci., 380, 109379, 2025
[40] Stability of stationary states for mean field models with multichromatic interaction potentials
B. Bertoli, B. D. Goddard, and G. A. Pavliotis
IMA J. Appl. Math., 89(5), 833-859, 2025
[39] MultiShape: a spectral element method, with applications to Dynamic Density Functional Theory and PDE-constrained optimization
J. C. Roden, R. D. Mills-Williams, J. W. Pearson, and B. D. Goddard
IMA J. Num. Anal., 45(4), 2470-2504, 2025
[38] Hydrodynamic density-functional theory for the moving contact-line problem reveals fluid structure and emergence of a spatially distinct pattern
A. Nold, B. D. Goddard, D. N. Sibley, and S. Kalliadasis
Phys. Rev. Fluid., 9, 124003, 2024
[37] Experimental and theoretical bulk phase diagram and interfacial tension of ouzo
A. J. Archer, B. D. Goddard, D. N. Sibley, J. T. Rawlings, R. Broadhurst, F. F. Ouali, and D .J. Fairhurst
Soft Matt., 20, 5889-5903, 2024
[36] Virtual Maths Circles: helping young people to think like researchers
F. Iezzi, B. D. Goddard, and M. O’Brien
Res. All., 8(1), 2, 2024
[35] Dynamic density functional theory with inertia and background flow
R. D. Mills-Williams, B. D. Goddard, and A. J. Archer
J. Chem. Phys., 160, 174901, 2024
[34] Binding potential and wetting behavior of binary liquid mixtures on surfaces
M. Areshi, D. Tseluiko, U. Thiele, B. D. Goddard, and A. J. Archer
Phys. Rev. E, 109, 024801, 2024
[33] Stability of nanoparticle laden aerosol liquid droplets
A. J. Archer, B. D. Goddard, and R. Roth
J. Chem. Phys, 159, 194503, 2023
[32] Dynamic density functional theory for sedimentation processes on complex domains: Modelling, spectral elements, and control problems
J. C. Roden, B. D. Goddard, and J. W. Pearson
J. Chem. Phys, 159, 154102, 2023
[31] On the study of slow-fast dynamics, when the fast process has multiple invariant measures
B. D. Goddard, M. Ottobre, K. J. Painter, and I. Souttar
Proc. R. Soc. A 479, 20230322, 2023
[30] Improving tobacco social contagion models using agent-based simulations on networks
A. Prabhakaran, V. Restocchi, and B. D. Goddard
ANS, 8, 54, 2023
[29] Non-mean-field Vicsek-type models for collective behavior
P. Buttà, B. D. Goddard, T. M. Hodgson, M. Ottobre, and K. J. Painter
M3AS, 32(14), 2763-2816, 2022
[28] Pseudospectral methods and iterative solvers for optimization problems from multiscale particle dynamics
M. Aduamoah, B. D. Goddard, J. W. Pearson, and J. C. Roden
BIT Num. Math., 62, 1703–1743, 2022
[27] Noisy bounded confidence models for opinion dynamics: the effect of boundary conditions on phase transitions
B. D. Goddard, B. Gooding, G. A. Pavliotis, and H. Short
IMA J. Appl. Math., 87(1) 80–110, 2022
[26] Modelling inelastic granular media using Dynamical Density Functional Theory
B. D. Goddard, T. D. Hurst, and R. Occone
J. Stat. Phys., 183(1) 1–22, 2021
[25] A derivation of the Liouville equation for hard particle dynamics with non-conservative interactions
B. D. Goddard, T. D. Hurst, and M. Wilkinson
Proc. Roy. Soc. Edin. A, 151(3), 1040–1074, 2021
[24] Nascent transcript folding plays a major role in determining RNA polymerase elongation rates
T. W. Turowski, E. Petfalski, B. D. Goddard, S. L. French, A. Helwak, and D. Tollervey
Mol. Cell, 79, 1–16, 2020
[23] The singular hydrodynamic interactions between two spheres in Stokes flow
B. D. Goddard, R. D. Mills-Williams, and J. Sun
Phys. Fluids, 32, 062001, 2020
[22] Nonadiabatic transitions in multiple dimensions
V. Betz, B. D. Goddard, and T. Hurst
SIAM J. Sci. Comp., 41, (5), B1011-B1033, 2019
[21] Automated calculation of higher order partial differential equation constrained derivative information
J. R. Maddison, D. N. Goldberg and B. D. Goddard
SIAM J. Sci. Comp., 41, (5), C417-C445, 2019
[20] The vicinity of an equilibrium three-phase contact line using density functional theory: Density profiles normal to the fluid interface
A. Nold, L . G . MacDowell, D. N. Sibley, B. D. Goddard and S. Kalliadasis
Mol. Phys., 116, (17), 2239-2243, 2018
[19] General framework for fluctuating dynamic density functional theory
M. A. Duran-Olivencia, P. Yatsyshin, B. D. Goddard and S. Kalliadasis
New. J. Phys., 19, 123022, 2017
[18] Nonequilibrium molecular dynamics simulations of nanoconfined fluids at solid-liquid interfaces
M. Morciano, M. Fasano, A. Nold, C. Braga, P. Yatsyshin, D. N. Sibley, B. D. Goddard, E. Chiavazzo, P. Asinari, and S. Kalliadasis
J. Chem. Phys., 146, 244507, 2017
[17] Pseudospectral methods for density functional theory in bounded and unbounded domains
A. Nold, B. D. Goddard, P. Yatsyshin, N. Savva and S. Kalliadasis
J. Comp. Phys., 334, 639-664, 2017
[16] Dynamical density functional theory with hydrodynamic interactions in confined geometries
B. D. Goddard, A. Nold and S. Kalliadasis
J. Chem. Phys., 145, 214106, 2017
[15] Dynamical density functional theory for orientable colloids including inertia and hydrodynamic interactions
M. A. Duran-Olivencia, B. D. Goddard and S. Kalliadasis
J. Stat. Phys., 164, (4), 785-809, 2016
[14] Wave packet dynamics in the optimal superadiabatic approximation
V. Betz, B. D. Goddard and U. Manthe
J. Chem. Phys., 144, 224109, 2016
[13] Nanoscale fluid structure of liquid-solid-vapour contact lines for a wide range of contact angles
A. Nold, D. N. Sibley, B. D. Goddard and S. Kalliadasis
Math. Model. Nat. Phenom., 19, (4), 111-124, 2015
[12] Fluid structure in the immediate vicinity of an equilibrium three-phase contact line and assessment of disjoining pressure models using density functional theory
A. Nold, D. N. Sibley, B. D. Goddard and S. Kalliadasis
Phys. Fluids, 26, 72001, 2014
[11] Multi-species dynamical density functional theory
B. D. Goddard, A. Nold and S. Kalliadasis
J. Chem. Phys., 138, 144904, 2013
[10] Unification of dynamic density functional theory for colloidal fluids to include inertia and hydrodynamic interactions: Derivation and numerical experiments
B. D. Goddard, A. Nold, N. Savva and S. Kalliadasis
J. Phys.: Condens. Matter, 25, 35101, 2013
[9] General dynamical density functional theory for classical fluids
B. D. Goddard, A. Nold, N.Savva, G. A. Pavliotis and S. Kalliadasis
Phys. Rev. Lett., 109, 120603, 2012
[8] The overdamped limit of dynamic density functional theory: Rigorous results
B. D. Goddard, G. A. Pavliotis and S. Kalliadasis
SIAM Multiscale Model. Sim., 10, (2), 633-663, 2012
[7] Nonadiabatic transitions through tilted avoided crossings
V. Betz and B. D. Goddard
SIAM J. Sci. Comp., 33, (5), 2247-2276, 2011
[6] Atomic structure via highly charged ions and their exact quantum states
G. Friesecke and B. D. Goddard
Phys. Rev. A, 81, 32516, 2010
[5] Accurate prediction of non-adiabatic transitions through avoided crossings
V. Betz and B. D. Goddard
Phys. Rev. Lett., 103, 213001, 2009
[4] Superadiabatic transitions in quantum molecular dynamics
V. Betz, B. D. Goddard and S. Teufel
P. Roy. Soc. A-Math. Phy., 485, 3553-3580, 2009
[3] Asymptotics-based CI models for atoms: Properties, exact solution of a minimal model for Li to Ne, and application to atomic spectra
G. Friesecke and B. D. Goddard
SIAM Multiscale Model. Sim., 7, (4), 1876-1897, 2009
[2] Explicit large nuclear charge limit of electronic ground states for Li, Be, B, C, N, O, F, Ne and basic aspects of the periodic table
G. Friesecke and B. D. Goddard
SIAM J. Math. Anal., 41, (2), 631-664, 2009
[1] Rate of convergence of the configuration interaction model for the helium ground state
B. D. Goddard
SIAM J. Math. Anal., 41, (1), 77-116, 2009