I am interested in the derivation and analysis of reduced models for complex physical systems. In particular, I use a synergistic approach combining modelling, mathematical analysis and numerics to study phenomena in a wide range of mathematical physics including soft matter, granular media, quantum molecular dynamics, and the electronic structure of atoms and molecules. I also have strong interests in numerical methods, in particular pseudospectral methods. I have also worked on a range of other applications, including mathematical biology, PDE-constrained optimisation, opinion dynamics.
Soft matter is a broad (and, for a mathematician’s point of view, poorly defined) term that describes materials that are easily deformed under the application of external forces, such as gravity or pressure, at room temperature Typical everyday examples include soaps, gels, foams, paints, gels, liquid crystals and biological matter. The aim of this research is to understand and elucidate the fundamental physics behind the behaviour of such materials both in and our of equilibrium.
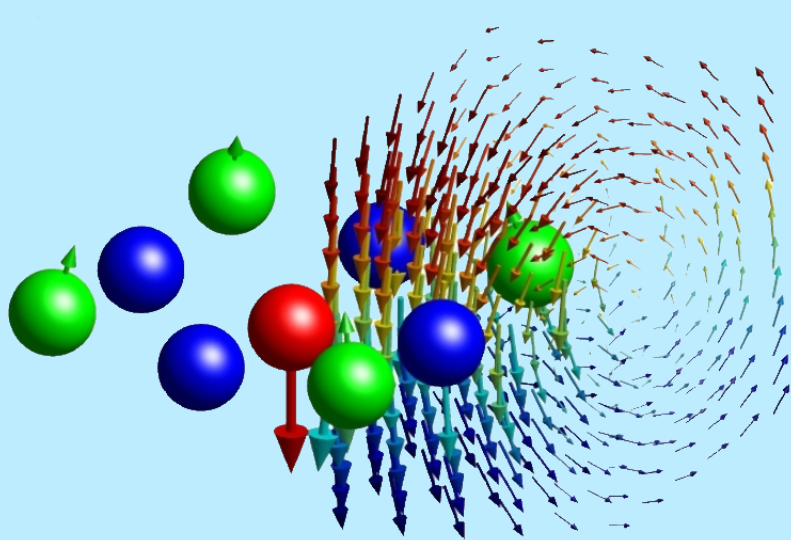
Such effects are highly multiscale since interactions on the microscopic, particle-size scale strongly affect the macroscopic behaviour. These problems require a careful combination of modelling, rigorous mathematical analysis and numerics. Since the experimental observation of Brownian motion in the 19th century and the foundation of statistical mechanics by Einstein at the start of the 20th century, colloidal fluids (consisting of many microscopic particles suspended in a fluid bath) have been model systems for both experimental and theoretical scrutiny. Typical examples of colloidal fluids are milk, blood and ink, and recent advances in biophysics and nanotechnology have stimulated great interest in the dynamics of soft matter.
Due to the large numbers of particles, direct computation of the dynamics becomes intractable and reduced models are necessary. Ideally, we would like reduced equations with dimension independent of the number of particles. In recent years one such class of models, known as dynamical density functional theories (DDFTs), has received increasing attention. Existing DDFTs neglect either the inertia of the colloidal particles, or hydrodynamic interactions (bath-mediated forces), or both. However, these effects are crucial for understanding the dynamics of many colloidal systems and a more general DDFT is required.
My work focuses on the derivation and numerical solution of DDFT models. I am particularly interested in physical effects which are not included in ‘standard’ DDFT, such as inertia, hydrodynamic interactions, and flows in the bath. The DDFTs we work with contain many other formalisms as special cases. I take two main approaches for the numerical solution of DDFTs, which typically are nonlocal, nonlinear PDEs: (i) continuum models and pseudospectral methods; (ii) lattice models.
I am also interested in rigorous results concerning DDFT and DDFT-like equations. Via a rigorous homogenization argument, we have shown that the true DDFT in the high friction limit differs from that obtained by more heuristic arguments. In particular, the rigorously-derived DDFT included a density-dependent diffusion tensor. We have also worked on classifying possible stationary states of systems with complex interaction potentials.
Joint work with Andrew Archer (Loughborough University, Maths), Joe Brader (University of Fribourg, Physics) Serafim Kalliadasis (Imperial College London, Chem. Eng.), Andreas Nold (Max Plank Institute for Brain Research), Raffaella Ocone (Heriot-Watt University, Engineering), Greg Pavliotis (Imperial College London, Maths), Nikos Savva (University of Cyprus, Maths), David Sibley (Loughborough University, Maths), Jin Sun (University of Glasgow, Engineering), Job Thijssen (University of Edinburgh, Physics), Salomée Tschopp (University of Fribourg, Physics) Mark Wilkinson (Nottingham Trent University, Maths), Petr Yatsyshin (Imperial College London, Chem. Eng.), and numerous PhD students.
In joint work with mathematicians and experimental physicists, we have been combining modelling and experiment to understand the behaviour of ouzo and similar spirits. These have fascinating properties, in particular the spontaneous formation of long-lived emulsions (i.e, why ouzo goes, and stays, cloudy when you add water).
Joint work with Andrew Archer (Loughborough University, Maths), Dave Fairhurst (University of Edinburgh, Physics) Fouzia Ouali (Nottingham Trent University, Physics), and David Sibley (Loughborough University, Maths).
We have developed an extensive suite of codes to solve problems using pseudospectral methods. Although our main focus has been on the solution of nonlinear, nonlocal PDEs, the methods we have developed are very widely applicable. We have tools to efficiently and accurately tackle such problems in 1D, 2D, and (for basic problems) 3D. We have also developed a spectral element approach (in both 1D and 2D), which is particularly well-suited to treating industrial problems due to its ability to solve complex problems on complicated geometries to a very high level of accuracy.
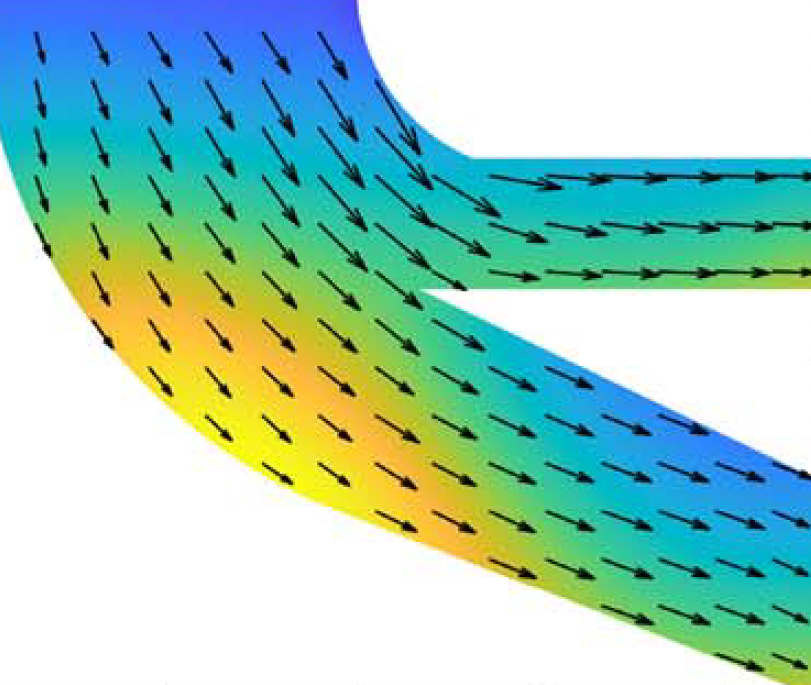
Psudeospectral methods are appropriate for problems where the solution has a very high degree of regularity (smoothness), and where the domain is relatively simple (e.g., composed of quadrilaterals, wedges, parts of discs, etc). In such cases, the convergence of differentiation and integration is ‘spectrally accurate’ - the methods converge with an error that decays exponentially in the number of grid points. This contrasts with more standard approaches, such as finite element or finite difference, where errors are typically bounded by a small negative power of the number of grid points. Crucially for DDFT and other, similar, applications, pseudospectral methods use small, dense matrices. The nonlocal operators (such as convolutions) require dense matrices in any numerical scheme; this destroys many of the advantages of approaches such as finite element (which relies on large, sparse matrices), but has very little effect on the efficiency or accuracy of pseudospectral approaches.
Joint work with Andreas Nold (Max Plank Institute for Brain Research), and numerous PhD students.
Granular media is a term used to describe collections of discrete, typically hard, particles, such as sand, cereals, pharmaceutical tablets, and rocks. Examples occur over a huge range of length scales, and such materials exhibit complex behaviours such as transitioning between solid- and liquid-like behaviours, avalanches, and segregation. The key difference between granular media and soft matter is that the effects of the liquid bath are typically ignored in granular media; the particles are assumed to be ‘dry’. However, many interesting scientific and industrial questions arise when some amount of liquid is added to the system. Consider the very different behaviour between dry rice out of a packet and damp rice that has just been washed.
We have been working to extend DDFT to granular media (in which the bath has very low, or even zero, viscosity). We have derived an associated DDFT which requires externally-determined parameters. Through a combination of microscopic simulations and data-science approaches, we have determined appropriate values for these parameters and numerically implemented the associated DDFTs. This has allowed us to elucidate the important physical effects in inelastic granular media.
For wet granular media, the principal additional physics comes from hydrodynamic interactions. Generally, short-range interactions (known as lubrication forces) are thought to dominate. These interactions describe the effect of the liquid on the particles. Consider, for example, trying to push together two particles in liquid. Compared to the dry system, one has to do extra work to move the fluid out of the way. Such lubrication forces can qualitatively affect the dynamics of wet granular systems. Following some theoretical work on the form of hydrodynamic interactions, I have also been collaborating with an industrial partner to implement our approach, and analogous results from the literature, in order to more accurately model these systems. A key application is in battery manufacturing, where electrodes are often made from pastes, which are well-described by our approaches.
Joint work with Raffaella Ocone (Heriot-Watt University, Engineering), previous PhD students, and Altair EDEM.
We are interested in understanding how people form and change their opinions. This is a highly interdisciplinary topic with many modelling approaches. We have primarily been interested in so-called ‘bounded confidence’ models. In such models, one updates their opinion by considering the opinions of others and moving to(wards) the average of those opinions. If the model contains no other effects then this always leads to a single cluster of opinions, which is known not the be realistic in most situations. What instead is done is to introduce a ‘confidence bound’. People whose opinions are further away than this confidence bound are ignored when computing the average. This models people ignoring the views of others whose opinions on a topic are too different from theirs. This effect is particularly obvious in many political discussions. Such models reproduce the clustering of opinions that is often found in data and can reproduce other effects, such as typical distributions of opinions over time in referenda.
We have looked at ODE, SDE, and PDE models, as well as those on networks. We are primarily interested in the PDE models, in part because they describe what happens ‘on average’, without having to know precise initial conditions which are often challenging to obtain, but also because there are strong links to DDFT in both modelling and numerics. The PDE approach also allows us to undertake rigorous mathematical analysis of the models, including identifying critical values for the interaction strength above which clusters typically form.
Joint work with Greg Pavliotis (Imperial College London, Maths) and Valerio Restocchi (University of Edinburgh, Informatics).
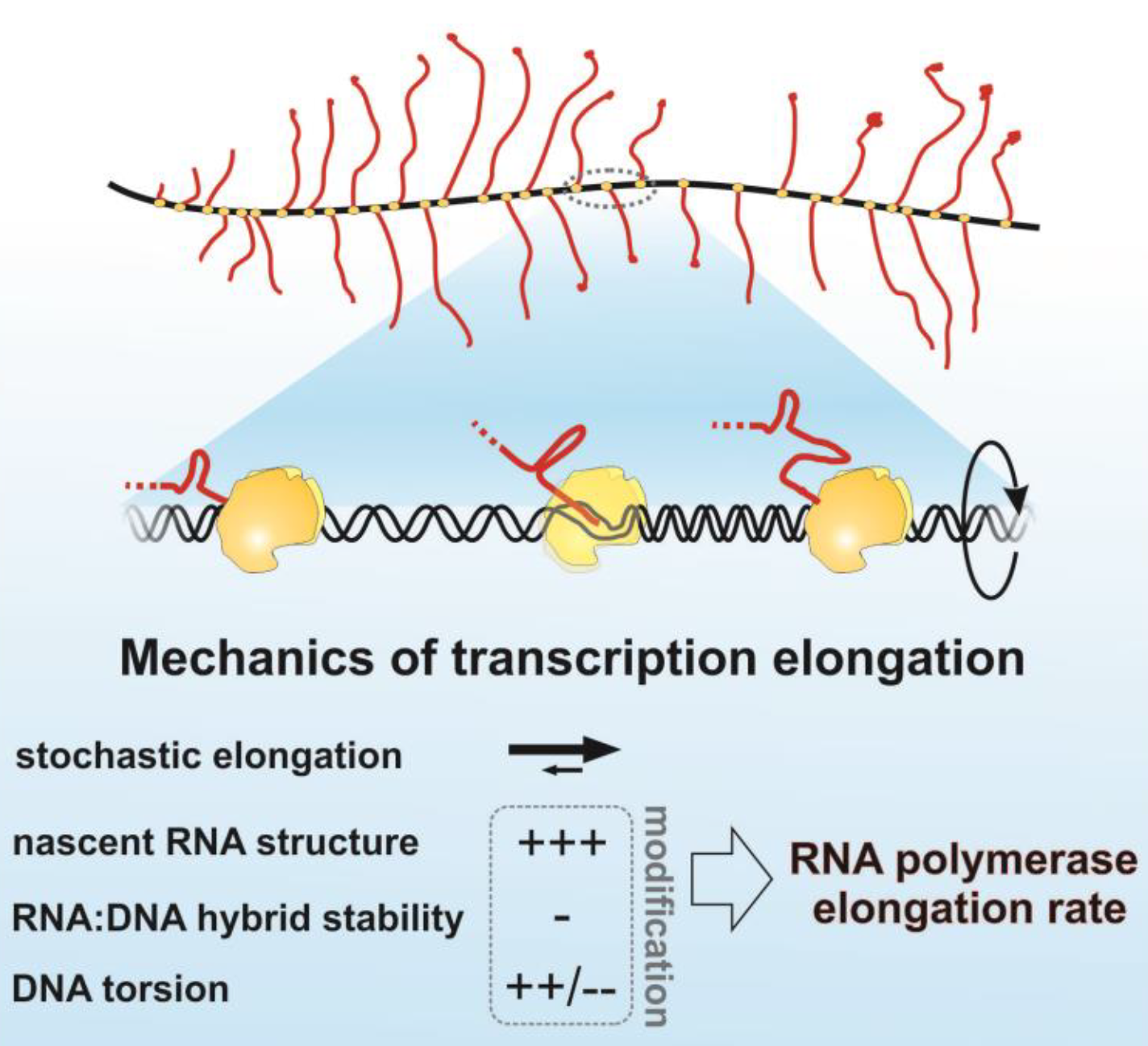
We are studying the effects of transcription elongation rates on RNA processing. Generally, sequence-specific regulation is poorly understood. We are using a combination of in vivo experiments (done by my collaborators, so, thankfully, I don’t need to go anywhere near a lab) and in silico (i.e., computational) studies to elucidate some commonly-observed features of RNA transcription. In particular, we focus on the uneven local polymerase occupancy (which suggests a substantial variation in transcription speed), and correlation of forward translocation with the folding energy. Our mathematical model uses a stochastic jump process to model the interacting RNA polymerases as they transcribe along the RNA. We find that the agreement between experiment and theory is very good, with almost all parameters in the model being determined experimentally (i.e., we haven’t just fitted an elephant).
It is interesting to see that a relatively simple mathematical model (from my point of view, not necessarily a feeling shared by the biologists) can lead to very good agreement with experiment. There are many interesting possible extensions to this work, which we hope to pursue in the near future.
Joint work with David Tollervey and Tomasz Turowski (University of Edinburgh, Wellcome Centre for Cell Biology).
We are using a range of methods to understand the spread of both diseases (as is typically done in mathematical biology), and also of smoking, which can be thought of as an infectious habit, where interactions with other people (and external factors) affect the probability of an individual starting, stopping, or relapsing into smoking. We have use approaches inspired by the famous SIR models, along with a spatial dependence, as well as network-based approaches. The former is well-suited to be coupled to data and optimization approaches to parameterize the model, especially when combined with powerful numerical approaches such as pseudospectral methods. The latter allows one to make policy recommendations as to how to reduce smoking prevalence. The key here is that we do not need extensive knowledge of the underlying network and can, instead, make general recommendations underpinned by modelling, social theory, and extensive numerical simulations.
Joint work with Valerio Restocchi (University of Edinburgh, Informatics).
One of the most common way of modelling large-scale physical systems is through the use of partial differential equations (PDEs); in particular, they can be used to model systems of interacting particles, such as molecules, cells, people, or stars. There are many situations in which these systems can be controlled, for example though the use of external forces, or by the design of engineering devices. Generally, there will be a desired target distribution of the particles, for example separating them based on size, or achieving rapid sedimentation under gravity. A major challenge is to determine the optimal way in which to control these processes. Here, optimal reflects some balance between the distance of the solution from the target state and the cost, be it in terms of time, financial cost, or resources. Mathematically, these problems are formulated in terms of PDE-constrained optimisation (PDECO).
Most mathematical work on PDECO has focussed on systems in which inter-particle interactions are neglected. In some situations this is a reasonable assumption. However, in many cases, the inter-particle interactions are one of the dominant effects in the system and qualitatively and quantitatively affect the dynamics. For example, the attraction of yeast cells causes them to clump together (or flocculate), which significantly affects the sedimentation dynamics in the brewing process.
We are working to combine models from DDFT (which provide accurate solutions to the dynamics of interacting particles) with techniques from PDECO in order to tackle real-world, industrially-relevant applications.
Joint work with James Maddison and John Pearson (University of Edinburgh, School of Mathematics).
The aim of quantum molecular dynamics is to solve the time-dependent Schrödinger equation, which describes the motion of the electrons and nuclei in atoms and molecules. Since nuclei are much (at least a few thousand) times heavier than electrons, the timescales associated with the motion of nuclei and electrons are generally well-separated. In particular, when electronic energy levels for a given molecule are well-separated, the nuclear and electronic dynamics decouple, leading to the Born-Oppenheimer approximation under which the electrons are assumed to equilibrate instantaneously from the point of view of the nuclei. This dramatically reduces the complexity of the problem (however, it is still hard!).
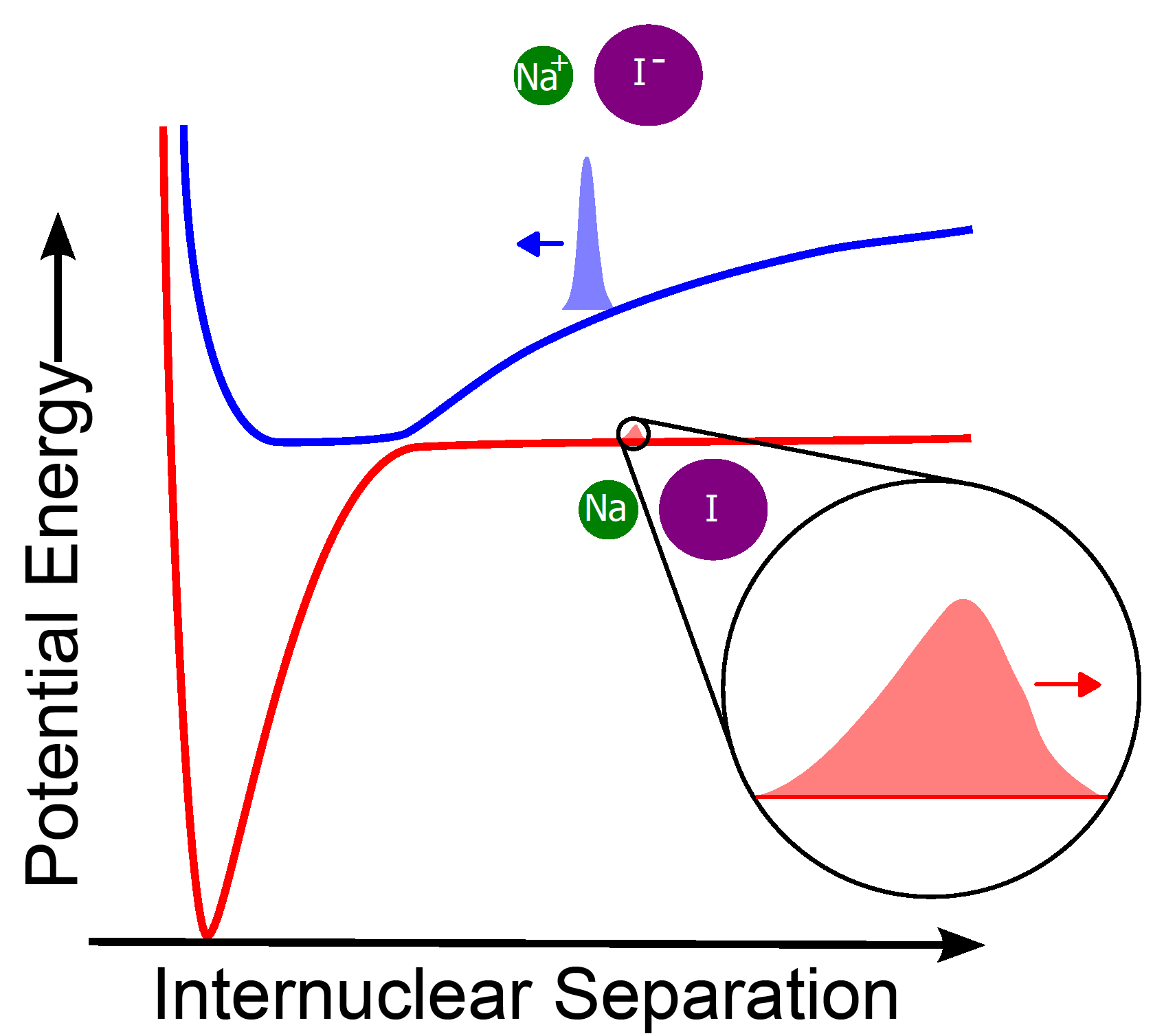
Despite its success, situations in which the Born-Oppenheimer approximation fails are of great interest in quantum chemistry. These occur when the electronic energy levels are not well-separated for a given nuclear configuration. Important applications include the photodissociation of diatomic molecules like NaI (sodium iodide), or the reception of light in the retina. Two basic types of failure occur: conical (or full) crossings as appearing, and avoided crossings. The latter are typical for systems with one nuclear degree of freedom, and are the topic of much of our research.
The simplest example of such a system is a dimer (a molecule with two atoms, such as NaI) for which we consider only the interatomic separation. This is a 1D problem and, for a particular separation, the lowest two energy levels become very close but do not cross. In a typical experiment, a laser excites the electrons, which change configuration. This in turn causes a force on the nuclei, causing them to move apart. When the electronic energy levels are well-separated, the Born-Oppenheimer approximation is very accurate and only the dynamics on the excited energy level need to be considered. However, near the avoided crossing, the energy levels couple and an exponentially small part of the wavepacket is transferred to the lower energy level. This purely quantum effect is crucial in many ultrafast reactions.
To understand such processes, it is crucial to be able to predict the size and shape of the transmitted wavepacket. The main difficulties are that it is both exponentially small (meaning that numerical errors are likely to swamp the true result) and very quickly oscillating (meaning that a very fine grid is needed). Hence such problems are numerically highly challenging. Our work bypassed this issue via careful application of a mathematical technique called superadiabatic projections. This allowed us to derive an explicit formula for the transmitted wavepacket. This led to the determination of an efficient and accurate algorithm, the result of which agrees with highly-accurate numerical simulations for a wide range of wavepackets and potentials. We have recently extended our results to arbitrary dimension (degrees of freedom), and demonstrated the excellent accuracy in 2D.
Joint work with Volker Betz (TU Darmstadt, Maths), Adam Kirrander (University of Edinburgh, Chemistry), Caroline Lasser (TU Munich, Mathematics), Uwe Manthe (Universität Bielefeld, Chemistry), and Stefan Teufel (Universität Tübingen, Maths).
The principal aim of quantum chemistry is to solve the (non-relativistic, Born-Oppenheimer) electronic Schrödinger equation. To paraphrase Dirac, in principle, this allows the prediction of all chemical and physical properties of the system. However, due to the dimension scaling exponentially with the number of particles, standard numerical techniques are unsuitable, and an approximate model must be treated. In addition, this is a tough multi-scale problem; interest lies not in absolute energies, but in energy differences, which are generally several orders of magnitude smaller.

Although very successful, most numerical methods are based on chemical intuition and computational experience. In addition, the best calculated wavefunctions are linear combinations of millions or even billions of Slater determinants (N-particle basis functions). This presents major problems when trying to analyse such wavefunctions, and in interpreting them in terms of standard textbook chemistry models, such as orbital shell filling (the Aufbau principle).
We have shown that many of the interesting chemical properties of small atoms and ions can be demonstrated through the `PT model’, based on first order perturbation theory. This model consists of fixing the number of electrons (which determine the chemistry) and increasing the nuclear charge. Such sequences of ions are realised in nature, which allows us to compare directly to experiment. We find that, for moderately charged ions, our model produces highly accurate results. In addition, this approximation is exactly soluble, by hand! This is somewhat surprising as, for the case of Carbon, it requires diagonalizing a 70×70 matrix. The resulting simple wavefunctions can be written out explicitly and lead to increased insight into the fundamental physics and chemistry underlying the behaviour of atoms.
By suggesting a novel scaling in which to plot energies of isoelectronic sequences, our results led to the identification of incorrectly assigned experimental results for five-electron ions. It also allows, through cubic spline fitting, to predict the values of missing experimental energy levels, and for some empirical chemical observations to be studied rigorously. For example, asymptotic ground states differ from those traditionally described in chemistry, by small but interesting corrections, which dramatically alter properties such as relative electron positions, providing insight into chemical bond angles.
Unfortunately, for neutral atoms the energies produced by this model are not chemically accurate. This is a result of its failure to satisfy the virial theorem, which enforces a ratio of the kinetic and potential energies. We therefore extended the model by introducing three variational parameters (analogous to widely-used ‘screening parameters’), producing the first mathematical definition of a Configuration Interaction model. This model is ‘minimal’ in the sense that it contains the smallest basis, with the fewest parameters, such that it is symmetry preserving, asymptotically exact, and satisfies the virial theorem. Up to minimization over the three parameters, it remains exactly soluble by hand. The energies obtained for atoms are comparable to (and in some cases better than) those of much larger numerical models.
Our simple wavefunctions and a novel definition of bond angle in a trimer with two hydrogen atoms and a central atom X, allowed us to accurately predict, from first principles, the H-X-H bond angles. This angle depends on the bond length and, for a number of cases is not unique (a consequence of the non-uniqueness of the ground state) and thus we predict a continuous range of possible bond angles, all with the same energy of the central atom. Atoms with such bond angle ranges can be thought of as more ‘flexible’ and thus able to form a greater range of bonds (i.e. molecular geometries), with no energy penalty to the central atom. For sensible choices of the bond length, the predicted bond angles agree well with experiment for all first row atoms. In addition, we have shown that the small corrections to the standard Aufbau model are critical in predicting these bond angles.
Joint work with Gero Friesecke (TU Munich, Mathematics).